Part 1 Bonus Material
No-Nonsense Quantum Mechanics
- For an alternative explanation of the double-slit experiment see Surfing and the double-slit experiment by Brian Skinner.
- An especially nice video explanation of the quantum uncertainty is this one by 3Blue1Brown.
- For a deeper discussion of experimental aspects of the uncertainty principle and how it is interpreted in modern terms see page 93ff in Quantum Theory: Concepts and Methods by Peres.
- We actually get an uncertainty principle like we do in Quantum Mechanics whenever our system has something to do with waves. The quantum uncertainty is a special case of the more general bandwidth theorem for waves. For a nice discussion, see page 236ff in Georgi’s Physics of Waves, which is available freely online.
Exercises
What do we learn from the double slit experiment? How do we come to this conclusion?
Although elementary particles are discrete things (we observe "click click click" in our detectors), we need waves to describe them.
Surprisingly, we observe for elementary particles like electrons an interference pattern, which we usually only expect for waves like water waves. For classical discrete objects like balls or objects, we don't get an interference pattern. Most of them end up around in the middle and progressively less as we move farther away from the middle. However, for waves, we get a sequence of maxima and minima.
How can we understand that quantization happens in Quantum Mechanics?
We can understand this by recalling the fundamental lesson of the double slit experiment: we need waves to describe particles. Wave naturally quantize quantities. Imagine a rope that is fixed at one end and with the other end in your hand. If you start swinging it, you can only produce a discrete set of wave modes. The allowed modes are quantized in discrete steps.
Similarly, in Quantum Mechanics the fact that we need waves to describe particles leads us naturally to the result that, for example, the energy levels of a particle in a box are quantized.
Why is there a fundamental uncertainty in Quantum Mechanics?
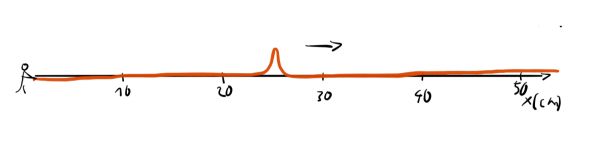 or a waveform with a well-defined wavelength:
or a waveform with a well-defined wavelength:
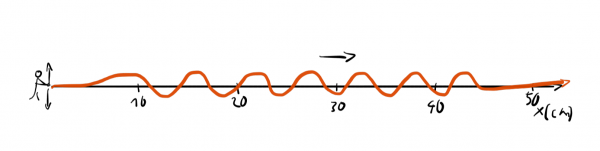 We can't assign one exact wavelength to a localized wave packet and we can't answer precisely where a wave with well-defined wavelength is.
We can't assign one exact wavelength to a localized wave packet and we can't answer precisely where a wave with well-defined wavelength is.
- Using the Fourier transform we can understand any localized wave package as a superposition of plane waves.
- Only plane waves have well-defined wavelengths, but only wave packages are localized. A plane wave spreads out all over space.
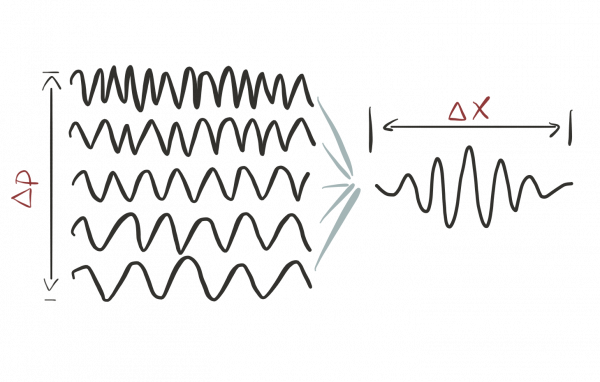 This tradeoff is described by the so-called bandwidth theorem and the quantum uncertainty is a special instance of this general result.
This tradeoff is described by the so-called bandwidth theorem and the quantum uncertainty is a special instance of this general result.What's an intuitive way to describe the quantum uncertainty?
"Heisenberg sometimes explained the uncertainty principle as a problem of making measurements. His most well-known thought experiment involved photographing an electron. To take the picture, a scientist might bounce a light particle off the electron's surface. That would reveal its position, but it would also impart energy to the electron, causing it to move. Learning about the electron's position would create uncertainty in its velocity; and the act of measurement would produce the uncertainty needed to satisfy the principle." - Scientific American "Bohr, for his part, explained uncertainty by pointing out that answering certain questions necessitates not answering others. To measure position, we need a stationary measuring object, like a fixed photographic plate. This plate defines a fixed frame of reference. To measure velocity, by contrast, we need an apparatus that allows for some recoil, and hence moveable parts. This experiment requires a movable frame. Testing one therefore means not testing the other." - NYTimes
Tossing a dice ten times yields: 2, 4, 1, 3, 3, 6, 3, 1, 4, 5. What's the expectation value?

On p. 22, there’s an illustration of what detection pattern we would expect if some macroscopic objects (bullets) were shot through the double slit. The result, according to the illustration, is that most of the bullets end up in the middle of the screen, with progressively less as we move away from the middle. But wouldn’t the expected result be that there are two bands, corresponding to the two slits, with progressively less trailing off to the sides, away from the middle, and slightly more in the exact center, where some bullets from both slits land?
Yes, you’re right. If the two slits are sufficiently far away from each other, we simply get two bands. Only when the distance between the two slits is small, the two bands overlap and most of the bullets end up in the middle.
I will modify the corresponding section to make this clearer.
Please let me know if you have any further questions or feedback.
The firing of each bullet may be considered a random event. Each trial is independent, as one event doesn’t directly depend on the other. The bullets choose which slit according to a fair coin toss. No information is available about what happens before the slit. So after entering one slit of the other, whatever scatters them is again a random trial of independent events. Over a long time, what we see on the wall/detector follows the Central Limit Theorem, and we get two overlapping Gaussian clouds. One Gausian cloud for each slit. They should have exactly the same standard deviation… Read more »
Jakob, First, great book. More on why later, but now in exercise 9 should not the value of e3 in new basis be – sqrt2 and not -2 as it is now.
Thanks a lot! I’ve corrected the typo.
Great Book! A question on operators and symmetries. Page 67 states
‘If a system does not change under spatial translations, we know momentum is conserved… If the system does not change under temporal translations we know energy is conserved.”
These two statements then lead to the derivation of the momentum and energy operators as listed on page 72.
I do not understand how these statements are obvious. Why would we know momentum and energy are conserved in these two instances?
Thanks! You’re right that these statements are far from obvious. They follow from Noether’s theorem. As mentioned in the text, Noether’s theorem is not discussed in detail since we only need the punchline and deriving it requires a discussion of the Lagrangian formulation of classical mechanics. But I’m about to finish a book on classical mechanics in which I discuss Noether’s theorem in detail. I will send you a copy via email as soon as it is finished.
On page 73, bottom paragraph, you wrote “$\partial_y x = 0$ but $\partial_y x = 1$”.
Thanks for reporting the typo. It should indeed read $\partial_y x = 0$.